Postingan ini menyajikan pembahasan soal UTBK 2019 pelajaran matematika. UTBK atau Ujian Tulis Berbasis Komputer merupakan tes masuk ke perguruan tinggi yang dilaksanakan oleh Lembaga Tes Masuk Perguruan Tinggi (LTMPT) sebagai satu-satunya lembaga penyelenggara tes perguruan tinggi terstandar di Indonesia.
Soal-soal UTBK matematika 2019 yang dibahas adalah soal-soal yang dipilih secara random. Jumlah semua soal yang dibahas adalah 20 soal, selebihnya mungkin akan dipos pada artikel selanjutnya. Oke, dibawah ini adalah pembahasan soal-soal UTBK matematika tahun 2019.
Soal 1 (eksponen)
Jika x memenuhi persamaan 3x + 2 – 3x = 32, maka nilai 45x
5x – 1= …
A. 9
B. 20
C. 45
D. 60
E. 80
Pembahasan
Untuk menjawab soal ini tentukan terlebih dahulu nilai x dengan cara sebagai berikut:
3x + 2 – 3x = 32
32 3x – 3x = 32
9 3x – 3x = 32
8 3x = 32
3x = 32/8 = 4
45x
5x – 1 = 9x . 5x
5x . 5-1
5 . (3x)2 = 5 . 42 = 5 . 16 = 80
Jadi soal ini jawabanya E.
Soal 2 (vektor)
Diketahui vektor-vektor a = (x + 1) i + x j, b = 2x i + (3x + 1) j dan p adalah proyeksi b dan a. Jika |p| ≤ 2 |a|, maka nilai x yang memenuhi adalah …
A. 0 ≤ x ≤ 2
B. 1 ≤ x ≤ 2
C. -2 ≤ x ≤ 3
D. -1 ≤ x ≤ 2
E. -2 ≤ x ≤ 2
Pembahasan

Jadi soal ini jawabannya D.
Soal 3 (fungsi)
Jika fungsi terdefinisi untuk x ≤ a atau x ≥ b, maka nilai a + b = …
A. 8
B. 5
C. 0
D. -5
E. -8
Pembahasan
Syarat agar akar terdefinisi adalah fungsi dalam akar ≥ 0 atau:
(x2 – 8x + 5) / (x2 + x + 12) ≥ 0
x2 – 8x + 5 ≥ 0
Dengan cara pemfaktoran:
… + … = -8
… x … = 5
Pada soal diatas fungsi terdefinisi untuk x ≤ a atau x ≥ b maka titik-titik diatas menunjukkan a dan b jadi:
a + b = -8
a x b = 5
Jadi a + b = -8 atau jawaban soal ini E.
Soal 4 (persamaan garis singgung)
Diberikan fungsi f(x) = 2x3 + 3x2 + 6x + 5. Garis singgung kurva y = f(x) dititik dengan absis x= a dan x = a + 1 saling sejajar. Jarak kedua garis singgung tersebut adalah…
A. 5/ √ 37
B. 4/ √ 37
C. 3/ √ 37
D. 2/ √ 37
E. 1/ √ 37
Pembahasan
m = f'(x) = 6x2 + 6x + 6
x = a maka m1 = 6a2 + 6a + 6
x = a + 1 maka m2 = 6(a + 1)2 + 6 (a + 1) + 6
6a2 + 12a + 6 + 6a + 6 + 6
6a2 + 18a + 18
Karena sejajar maka m1 = m2
6a2 + 6a + 6 = 6a2 + 18a + 18
6a – 18a = 18 – 6 atau – 12a = 12
a = -1
x1 = a = 1 dan y1 = 2 (-1)3 + 3 (-1)2 + 6 . -1 + 5 = 0
(x1 , y1) = (-1, 0)
x2 = a + 1 = – 1 + 1 = 0 dan y2 = 5
(x2 , y2) = (0 , 5)
m = 6 (-1)2 + 6 (-1) + 6 = 6
Persamaan garis 1 = y – y1 = m (x – x1) = y – 0 = 6 (x – (-1) = y – 6x – 1
Persamaan garis 2 = y – 5 = 6 (x – 0) = y – 6x – 5
Berdasarkan persamaan garis 1 dan 2 diketahui a = 1, b = -6, c = -1 dan d = -5 maka cara menghitung jarak dua garis singgung sebagai berikut:
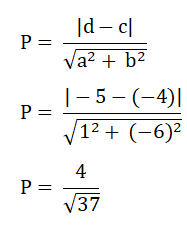
Jadi soal 4 jawabannya B.
Soal 5 (dimensi tiga)
Diberikan balok ABCD.EFGH memiliki panjang rusuk AB = 8, dan BC = CG = 6. Jika titik P terletak ditengah rusuk AB dan θ adalah sudut antara EP dan PG maka nilai cos θ adalah…
A. 3/ √ 286
B. 5/ √ 286
C. 0
D. -3/ √ 286
E. -5/ √ 286
Pembahasan
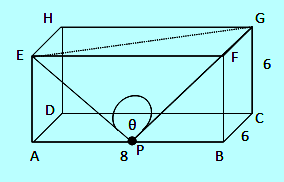
Hitung terlebih dahulu panjang EP2, PG2 dan EG2 dengan cara dibawah ini.
- EP2 = AP2 + AE2 = 42 + 62 = 52
- PG2 = CP2 + CG2 = 52 + 36 = 88
- EG2 = EF2 + GF2 = 64 + 36 = 100
Cara menghitung θ dengan menggunakan rumus cosinus sebagai berikut:
- EG2 = EP2 + PG2 – 2 EP PG cos θ
- 100 = 52 + 88 – 2 . √ 52 . √ 88 cos θ
- Cos θ = 5/ √ 286
Jadi soal ini jawabannya B.
Contoh soal 6 (simpangan rata-rata dan nilai rata-rata)
Bilangan-bilangan bulat a, a + 1, a + 1, 7, b, b, 9 telah diurutkan dari terkecil ke besar. Jika rata-rata semua bilangan itu adalah 7 dan simpangan rata-rata 8/7 maka a + b – 1 = …
A. 10
B. 11
C. 12
D. 13
E. 14
Pembahasan
Karena bilangan bulat dan telah diurutkan dari terkecil ke besar maka maka bilangan-bilangan tersebut adalah:
a, a + 1, a + 1, 7, b, b, 9
5, 6, 6, 7, 8, 8, 9
Jadi a = 5 dan b = 8
a + b – 1 = 8 + 5 – 1 = 12
Jadi soal ini jawabannya C.
Soal 7 (transformasi geometri)
Jika y = 2x + 1 digeser sejauh a satuan ke kanan dan b satuan ke bawah, kemudian dicerminkan terhadap sumbu X, bayangannya menjadi y = ax – b. Nilai a + b adalah…
A. -1/2
B. -3
C. 4
D. 3
E. 1/2
Pembahasan
Tranlasi garis oleh T(a, -b)
x’ = x + a atau x = x’ – a
y’ = y – b atau y = y’ + b
Subtitusi ke persamaan y = 2x + 1 sehingga didapat:
y’ + b = 2 (x’ – a) + 1 atau y’ = 2x’ – 2a – b + 1
Dicerminkan terhadap sumbu X hasilnya sebagai berikut:
x’ = x” dan y’ = – y”
-y” = 2x’ – 2a – b + 1 atau y” = -2x’ + 2a + b – 1
y” diganti menjadi y = ax – b diperoleh:
ax – b = -2x’ + 2a + b – 1
Jadi a = -2 dan -b = 2a + b – 1 atau -b = 2 . -2 + b – 1
b + b = 4 + 1 atau b = 5/2 = 2,5
Jadi nilai a + b = -2 + 2,5 = 0,5 = 1/2. Jadi soal ini jawabannya E.
Soal 8 (Peluang)
Didalam sebuah kotak terdapat m bola merah dan n bola putih dengan m + n = 16. Jika bola diambil sekaligus secara acak, maka peluang terambil dua bola tersebut berbeda warna adalah 1/2. Nilai dari m2 + n2 adalah…
A. 200
B. 160
C. 146
D. 136
E. 128
Pembahasan
Karena m + n = 16 maka n = 16 – m. Cara menjawab soal diatas sebagai berikut:

Jadi soal ini jawabanya D.
Soal 9 (Permutasi)
Dari angka 2, 4, 5, 6, 8, 9 akan dibentuk bilangan ganjil terdiri dari 3 digit berbeda. Banyak bilangan yang terbentuk yang nilainya kurang dari 500 adalah…
A. 144
B. 72
C. 24
D. 20
E. 16
Pembahasan
Susunan bilangan ganjil yang terdiri dari 3 digit dan kurang dari 500 yang dibentuk dari 2, 4, 5, 6, 8, 9 sebagai berikut:
2 … 5
2 … 9
4 … 5
4 … 9
Tiap titik-titik dapat diisi 4 angka lainnya (Misalkan 2 … 5 maka titik-titik dapat diisi oleh 4, 6, 8, 9). Jadi banyak bilangan yang dapat dibentuk = 4 x 4 = 16. Soal ini jawabannya E.
Soal 10 (Bunga Majemuk)
Ratna menabung di bank A dalam x tahun dan uangnya menjadi sebesar M. Wati juga menabung di bank A dalam x tahun dan uangnya menjadi 3 kali uangnya Ratna. Jika tabungan awal Wati sebesar Rp 2.700.000,00 dan bank A menerapkan sistem bungan majemuk, maka tabungan awal Ratna sebesar…
A. Rp 8.100.000,00
B. 5.000.000,00
C. 2.700.000,00
D. Rp 2.400.000,00
E. Rp 900.000,00
Pembahasan
Karena Ratna dan Wati menabung pada bank yang sama maka memperoleh bunga yang sama. Untuk menjawab soal ini kita menggunakan rumus perbandingan bunga majemuk sebagai berikut:

Soal nomor 9 jawabannya E.
Soal 11 (logaritma)
Himpunan penyelesaian dari pertidaksamaan (loga x)2 – loga x – 2 > 0 dengan 0 < a < 1 adalah…
A. x < a2 atau x > a-1
B. x < a2 atau x > a-2
C. a2 < x < a-1
D. a2 < x < a-2
E. a-2 < x < a2
Pembahasan
Cara menjawab soal ini kita misalkan loga x = m maka pertidaksamaan logaritma menjadi:
m2 – m – 2 > 0
(m – 2) (m + 1) > 0
m = 2 atau m = -1

m < -1 atau m > 2
alog x < -1 atau alog x > 2
x > a-1 atau x < a2
Jadi soal ini jawbannya A.
Soal 12 (limit)
A. 5/4
B. 7/4
C. 9/4
D. 11/4
E. 15/4
Pembahasan
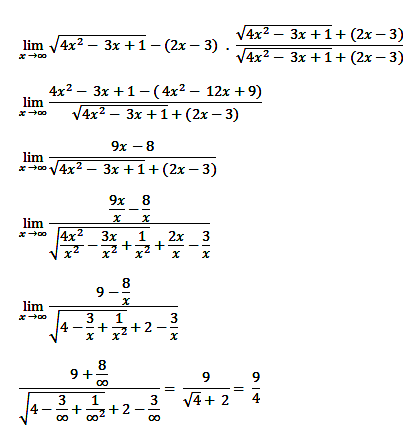
Soal ini jawabannya C.
Soal 13 (Suku banyak)
Suku banyak P(x) = x3 + bx2 – 2x – 6 habis dibagi (x – 2)2 bersisa -2x + a. Nilai a + b adalah…
a. 15
B. 13
C. 0
D. – 13
E. – 15
Pembahasan
Untuk menghitung a + b menggunakan cara susun. Pembagi (x – 2)2 = x2 – 4x + 4.

Jadi soal ini jawabannya D.
Soal 14 (Persamaan lingkaran)
Persamaan lingkaran yang pusatnya terletak pada garis 2x + 3y – 5 = 0 serta menyinggung sumbu X negatif dan sumbu Y positif adalah…
A. x2 + y2 + 10x – 10y + 25 = 0
B. x2 + y2 – 10x + 10y + 25 = 0
C. x2 + y2 – 10x + 10y – 15 = 0
D. x2 + y2 + 5x + 10y + 15 = 0
E. x2 + y2 + 5x – 10y + 15 = 0
Pembahasan
Titik pusat (a, b) = (-r, r)
2 . -r + 3 . r = 5 atau r = 5
Jadi titik pusat (a, b) = (-5, 5) dan jari-jari r = = 5
Persamaan lingkaran
(x – a)2 + (y – b)2 = r2
(x + 5)2 + (y – 5)2 = 52
x2 + y2 + 10x – 10y + 25 = 0
Soal ini jawabannya A.
Soal 15 (Barisan aritmetika)
Misalkan (Un) adalah barisan aritmetika dengan suku pertama a dan beda 2a. Jika U1 + U2 + U3 + U4 + U5 = 100, maka U2 + U4 + U6 + … + U20 = …
A. 720
B. 840
C. 960
D. 1080
E. 1200
Pembahasan
S5 = 1/2 n (2a + (n – 1) b
100 = 1/2 . 5 (2a + (5 – 1) 2a
100 = 2,5 (2a + 8a) = 2,5 . 10a
10 a = 100/2,5 = 40
a = 40/10 = 4
b = 2 a = 2 . 4 = 8
U1 = 4, U2 = 4 + 8 = 12, U3 = 12 + 8 = 20, U4 = 28 dan seterusnya. Jadi U2 + U4 + U6 + … + U20 mempunyai beda 2 . 8 = 16 dan jumlahnya sebagai berikut:
S10 = 1/2 n (2a + (n – 1) b)
S10 = 1/2 . 10 (2 . 12 + (10 – 1) 16)
S10 = 5 (24 + 144) = 840
Jadi soal ini jawabannya B.
Soal 16 (Matriks)

Pembahasan

Soal 17 (Trigonometri)
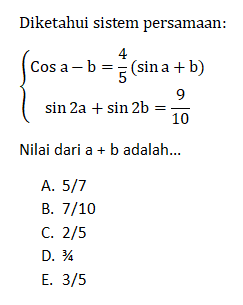
Pembahasan
Soal 18 (Integral)
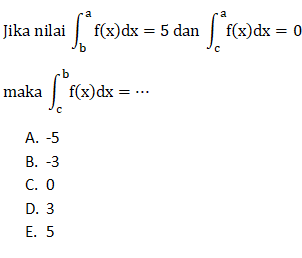
Pembahasan

Soal ini jawabanya E.
Soal 19 (Sistem persamaan)
Himpunan (x, y) adalah penyelesaian dari sistem persamaan:
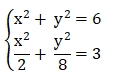
Jumlah dari semua nilai x dan y yang memenuhi adalah…
A. -2
B. -1
C. 0
D. 1
E. 2
Pembahasan
Persamaan kedua dikali 8 sehingga menjadi 4x2 + y2 = 24 atau y2 = 24 – 4x2. Subtitusi ke persamaan 1 sehingga didapat:
x2 + 24 – 4x2 = 6
-3x2 = 6 – 24 = – 18
x2 = -18/3 = 6 atau x = √ 6
y2 = 24 – 4 . 6 = 0 atau y = 0
Jadi dari semua nilai x dan y yang memenuhi adalah 0. Soal ini jawabannya C.
Soal 20 (pertidaksamaan nilai mutlak)
Himpunan penyelesaian dari |x – 1| < 3 – |x| adalah interval (a, b). Nilai 2a + b adalah…
A. -3
B. -2
C. 0
D. 2
E. 3
Pembahasan
|x – 1| = x – 1 jika x ≥ 1
|x – 1| = – (x – 1) jika x < 1
3 – |x| = 3 – x jika x ≥ 0
3 – |x| = 3 + x jika x < 0

x < 0
– (x – 1) < 3 + x
-x + 1 < 3 + x
-2x < 2
x > -1
0 < x < 1
-(x – 1) < 3 – x
-x + 1 < 3 – x
1 < 3 (bukan penyelesaian)
x > 0
x – 1 < 3 – x
2x < 4 atau x < 2
Jadi himpunan penyelesaiannya adalah -1 < x < 2. Dengan demikian nilai 2a + b = 2 . -1 + 2 = 0. Soal ini jawabannya C.