Kamis, September 21, 2023
Matematika

Contoh soal bangun datar yang sebangun dan kongruen

admin ,

Postingan ini membahas contoh soal bangun datar yang sebangun dan kongruen yang disertai pembahasannya. Bangun datar dikatakan kongruen jika memenuhi syarat yaitu memiliki ukuran-ukuran sisi yang bersesuaian yang sama dan memiliki ukuran-ukuran sudut yang bersesuaian yang sama. Jika dua buah bangun kongruen maka dipastikan kedua bangun tersebut sebangun.

Contoh soal 1

Diantara pasangan-pasangan bagun berikut, mana saja yang sebangun.

  1. dua buah segitiga sama kaki
  2. dua buah segitiga sama sisi
  3. dua buah persegi
  4. dua buah persegi panjang
  5. dua buah jajaran genjang
  6. dua buah layang-layang
  7. dua buah belah ketupat
  8. dua buah trapesium sama kaki
  9. dua buah segi lima beraturan

Pembahasan

  1. Dua buah segitiga sama kaki belum tentu sebangun karena perbandingan sisi-sisi bersesuaian belum tentu sama.
  2. Dua buah segitiga sama sisi dipastikan sebangun karena mempunyai sudut-sudutnya sama dan perbandingan sisi-sisi bersesuaian sama.
  3. Dua buah persegi dipastikan sebangun karena sudut-sudutnya sama dan perbandingan sisi-sisi bersesuaian sama.
  4. Dua buah persegi panjang belum tentu sebangun karena perbandingan sisi-sisi bersesuaian belum tentu sama.
  5. Dua buah jajaran genjang belum tentu sebangun karena perbandingan sisi-sisi bersesuaian belum tentu sama.
  6. Dua buah layang-layang belum tentu sebangun karena perbandingan sisi-sisi bersesuaian belum tentu sama.
  7. Dua buah belah ketupat belum tentu sebangun karena sudut-sudut yang bersesuaian belum tentu sama.
  8. Trapesium sama kaki belum tentu sebangun karena perbandingan sisi-sisi bersesuaian belum tentu sama.
  9. Segi lima beraturan dipastikan sebangun karena perbandingan sisi-sisi bersesuaian sama dan sudut-sudutnya sama.

Contoh soal 2

Perhatikan gambar kedua persegi panjang berikut ini.

Contoh soal bangun datar yang sebangun dan kongruen
Contoh soal 2 bangun datar yang sebangun dan kongruen

Jika AB = 12 cm, BC = 5 cm, LM = 5 cm dan KM = 13 cm maka buktikan bahwa:

  1. luas ABCD = luas KLMN
  2. keliling ABCD = keliling KLMN
  3. ABCD ≌ KLMN

Pembahasan

Jawaban soal 1:
Luas ABCD = panjang x lebar = AB x BC
Luar ABCD = 12 cm x 5 cm = 60 cm2
KL2 = KM2 – LM2 = 132 – 52
KL2 = 169 – 25 = 144 cm2
KL = √ 144   cm = 12 cm
Luas KLMN = KL x KM = 12 cm x 5 cm = 60 cm2
Luas ABCD = Luas KLMN = 60 cm2 (terbukti)

Jawaban soal 2
Keliling ABCD = 2 (AB + BC)
Keliling ABCD = 2 (12 cm + 5 cm) = 34 cm
Keliling KLMN = 2 (KL + LM) = 2 (12 cm + 5 cm) = 34 cm
Keliling ABCD = Keliling KLMN = 34 cm (terbukti)

Jawaban soal 3
Karena ABCD dan KLMN adalah persegi panjang maka sudut-sudut yang bersesuaian sama = 90°
AB : KL = 12 : 12 = 1 : 1
BC : LM = 5 : 5 = 1 : 1
Karena sudut-sudut bersesuaian sama dan perbandingan sisi-sisi bersesuaian juga sama maka bisa dipastikan persegi panjang ABCD ≌ KLMN.

Contoh soal 3

Contoh soal bangun datar yang sebangun dan kongruen
Contoh soal 3 bangun datar yang sebangun dan kongruen

Dari bangun-bangun tersebut, terhadap bangun (a), mana yang:

  1. Pasti sebangun
  2. Mungkin sebangun
  3. Tidak mungkin sebangun

Pembahasan

Jawaban soal 1:
Bangun yang sudah pasti sebangun dengan (a) adalah (d) karena:

  • sudut-sudut bersesuaian sama yaitu 124°, 56° dan dua sudut siku-siku.
  • Perbandingan sisi-sisi yang bersesuaian sama yaitu 8/4 = 2, 6/3 = 2, 12/6 = 2 dan 10/5 = 2.

Jawaban soal 2:
Bangun yang mungkin sebangun dengan (a) adalah (e) karena sudut-sudut bersesuaian sama yaitu 124°, 56° dan dua sudut siku-siku.

Jawaban soal 3
Bangun yang tidak mungkin sebangun dengan (a) adalah:

  • b karena perbandingan sisi-sisi yang bersesuaian berbeda yaitu 8/16 = 0,5 ; 6/11 = 0,545 ; 12/23 = 0,521; dan 10/16 = 0,625.
  • c karena sudut-sudut yang bersesuaian tidak sama.

Contoh soal 4

Contoh soal bangun datar yang sebangun dan kongruen
Contoh soal 4 bangun datar yang sebangun dan kongruen

Kedua segi empat pada gambar diatas adalah sebangun. Sebutkan:

  1. pasangan sudut-sudut yang sama besar
  2. pasangan sisi-sisi yang sebanding

Pembahasan

  1. pasangan sudut yang sama besar gambar diatas adalah y, x, z, o.
  2. pasangan sisi-sisi yang sebanding adalah AB dengan FG, AD dengan GH, BC dengan PE, dan CD dengan EH.

Contoh soal 5

Sebuah kusen jendela berukuran 75 cm x 125 cm terbuat dari kayu. Lebar kayu kusen disetiap sisinya sama yaitu 5 cm.

  1. Sketsa kusen tersebut
  2. Berapa ukuran bangun dalam kusen itu.
  3. Apakah persegi panjang tepi dalam kusen sebangun dengan persegi panjang tepi luarnya.

Pembahasan

Jawaban soal 1 sebagai berikut:

Sketsa kusen jendela

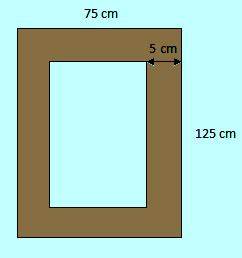
Jawaban soal 2:
Ukuran bangun dalam kusen:
75 cm – 5 cm – 5 cm = 65 cm
125 cm – 5 cm – 5 cm = 115 cm
Ukuran bangun dalam kusen adalah 65 cm x 115 cm.

Jawaban soal 3:
persegi panjang tepi dalam kusen tidak sebangun dengan persegi panjang tepi luarnya karena perbandingan sisi-sisi bersesuaian tidak sama yaitu 75/65 = 1,15 dan 125/115 = 1,08.

Contoh soal 6

Perhatikan gambar dibawah ini.

Contoh soal bangun datar yang sebangun dan kongruen
Contoh soal 6 bangun datar sebangun dan kongruen
  1. Tentukan panjang AF dan AC
  2. Tentukan panjang AB dan EB
  3. Apakah segi empat AEFG ≌ ABCD.

Pembahasan

Jawaban soal 1:
AF2 = AE2 + EF2
AF2 = 82 + 62 = 64 + 36 = 100 cm2
AF = √ 100   cm = 10 cm
Panjang AC = AF + FC = 10 cm + 5 cm = 15 cm

Jawaban soal 2:
AB2 = AC2 – BC2 = 152 – 92
AB2 = 225 – 81 = 144 cm2
AB = √ 144   cm = 12 cm
EB = 12 cm – 8 cm = 4 cm

Jawaban soal 3 : segiempat AEFG sebangun dengan segiempat ABCD karena:

  1. sudut-sudut bersesuaian sama besar yaitu 90 karena segi empat.
  2. perbandingan sisi-sisi bersesuaian sama yaitu AD : AG = 9 : 6 = 1,5 dan AB : AE = 12 : 8 = 1,5

Contoh soal 7

Perhatikan gambar dibawah ini.

Contoh soal bangun datar yang sebangun dan kongruen
Contoh soal 7

Selidiki persegi panjang manakah yang sebangun.

Pembahasan

Pada gambar diatas ada 3 persegi panjang yangitu ABCD, AFED dan FBCE. Perbandingan sisi-sisi bersesuaian ABCD dengan FBCE:
AD : FE = 9 : 9 = 1 : 1
AB : FB = 27 : 24 = 9 : 8
ABCD tidak sebangun dengan FBCE

Perbandingan sisi-sisi bersesuaian ABCD dengan AFED:
AD : AF = 9 : 3 = 3
AB : FE = 27 : 9 = 3
karena perbandingan sisi-sisi bersesuaian sama maka ABCD dengan AFED sebangun.

Perbandingan sisi-sisi bersesuaian AFED dengan FBCE:
AF : FE = 3 : 9 = 1 : 3
AD : FB = 9 : 24 = 3 : 8
AFED tidak sebangun dengan FBCE

Contoh soal 8

Perhatikan gambar dibawah ini.

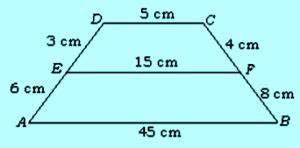
Contoh soal bangun datar yang sebangun dan kongruen
Contoh soal 8
  1. Apakah ABCD sebangun dengan DCFE, jelaskan.
  2. Apakah ABCD sebangun dengan ABFE, jelaskan.
  3. Apakah ABFE sebangun dengan DCFE, jelaskan.

Pembahasan

Jawaban soal 1:
AD : ED = 9 : 3 = 3
AB : EF = 45 : 15 = 3
BC : CF = 12 : 4 = 3
DC : DC = 5 : 5 = 1
ABCD tidak sebangun dengan DCFE.

Jawaban soal 2:
AD : AE = 9 : 6 = 3 : 2
AB : AB = 45 : 45 = 1
ABCD tidak sebangun dengan ABFE

Jawaban soal 3:AE : ED = 6 : 3 = 2
AB : EF = 45 : 15 = 3
BF : FC = 8 : 4 = 2
EF : DC = 15 : 5 = 3
ABFE tidak sebangun dengan DCFE.

Contoh soal 9

Contoh soal bangun datar yang sebangun dan kongruen
Contoh soal 9 bangun datar yang sebangun dan kongruen
  1. Buktikan PQT ≌ QRS
  2. Sebutkan pasangan-pasangan sisi dan sudut yang sama

Pembahasan

Jawaban soal 1:
PQ : QS = 5 : 5 = 1 : 1
QT : QR = (5 + 3) : 8 = 1 : 1
PT : RS = √ 52 + 82   : √ 52 + 82   = 1 : 1
Karena perbandingannya sama maka PQT ≌ QRS

Jawaban soal 2
Pasangan-pasangan sisi = QP = QS, QT = QR dan PT = SR
Sudut yang sama sudut PQT = sudut PQS, sudut QRS = sudut QTP dan sudut QPT = sudut QSR.

You cannot copy content of this page